Recrutement Google, étape #2

Mardi 28 novembre je me suis rendu dans les locaux de Google à Zürich afin de procéder à la suite du processus de recrutement. L'heure de rendez-vous, fixée à 10h00, n'étant pas trop contraignante, j'ai pris le train à Neyruz à 07h45 pour arriver à 09h38 à Zürich, et finalement 9h45 à Freigutstrasse 12, 8002 Zurich.

Le bâtiment est une ancienne banque privée, de couleur rosé et dont le style s'apparenterait au début du 20ème siècle. La porte d'entrée est fermée à clé, et il faut s'annoncer avant de pouvoir entrer. Puis une fois à l'intérieur, il faut s'inscrire sur un terminal et signer sur une tablette, et un badge autocollant est directement imprimé.

L'intérieur du bâtiment est plutôt blanc, avec du parquet sur le sol, mais ce qui frappe c'est les accessoires (poufs, ballons, coussins) de couleurs vives disposés un peu partout. On se croirait en plein jardin d'enfants. Seul les 2 écrans 20 pouces par place de travail rappellent qu'on est bien dans une entreprise de services.

Ma journée s'est composée de 4 entretiens techniques et d'un repas avec Peter, un des deux ingénieurs qui m'avait interviewé à l'EPFL.

Les questions posées étaient de nouveau très algorithmiques, principalement axées sur l'organisation des données en arbre ou table de hashage, tout en tenant compte de l'ordre de complexité des fonctions proposées.

Un exercice a retenu mon attention et je souhaite vous en faire partager mon expérience :

La donnée est simple : un personne se tient en bas d'un escalier de N marches. A chaque pas, il peut monter une ou deux marches. Combien de possibilités de configuration de trajets différents a-t-il pour monter l'escalier ?

L'illustration ci-dessous schématise le problème.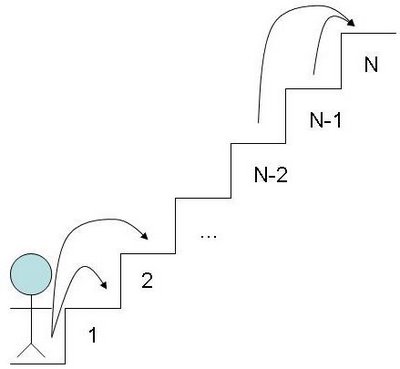


Le raisonnement approprié pour ce problème est de se dire que pour atteindre une marche n, la seule possibilité est d'être passé par la marche n-1 ou n-2, et donc le nombre de chemin pour arriver sur la marche n est la somme des possibilités d'arriver sur les cases n-1 et n-2.
On a donc la formule de récurrence suivante :
F_n = F_{n − 1} + F_{n − 2}
qui devrait nous faire penser à la suite de Fibonacci.

La suite de la question est simplement : comment peut-on calculer de manière efficace une telle suite ?

Il est possible de calculer une suite de Fibonacci de manière itérative, et donc d'une complexité de O(n), mais ce que je ne savais pas c'est qu'il existe une manière encore plus efficace pour calculer en O(log(n)) !

Cette solution repose sur deux propriétés : l'expression matricielle du problème, et le calcul de puissance.

La suite de Fibonacci peut donc s'exprimer sous la forme matricielle suivante :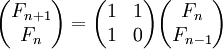


Ce qui nous amène à l'expression suivante :



On voit apparaitre un matrice 2x2 élevée à la puissance n. On peut donc utiliser l'algorithme square-and-multiply (donné ci-dessou) pour la calculée, qui lui est en O(log(n)).



CQFD. Des questions ? Des remarques ?

Je suis reparti vers 15h30, fatigué mais content. Je devrais avoir une réponse dans le courant de la semaine prochaine quant à leur envie de m'engager ou pas.

Suite au prochain (et peut-être dernier) épisode...

I'm the 58,920,569 richest person on earth!

Avec mon revenu actuel tout à fait moyen pour la Suisse (un peu moins de 4000.- brut / mois), je fais partie des 1% personnes les plus riches du monde, d'après le site GlobalRichList.

Imaginez ce que ça sera quand je toucherai mon salaire de ministre ;)

Plus sérieusement, voici une preuve criante que les richesses sont mal réparties.

Arriverons-nous à faire en sorte que la fossé qui sépare les riches des autres ne s'élargisse pas trop ? Un défi pour l'avenir autant important que l'environnement...

Bug de l'an 2038

Le format Unix pour les dates, c'est-à-dire le nombre de secondes depuis le 1er janvier 1970, est une très bonne chose car ça représentation est très compact, on peut facilement comparer 2 dates, calculer des intervalles, etc.

Le seul problème qui en découle est que son implémentation sous forme d'entier, 32 bits sur la majorité des systèmes actuels, et condamné à subir un integer overflow, et ce dans un peu plus de (2^^32 / 3600 / 24 / 365 =) 136 ans à partir de la date de référence si la date est codée en entier non signé, (2^^31 / 3600 / 24 / 365 =) 68 ans si le codage est signé, c'est-à-dire vers l'an 2106 ou 2038 respectivement.
Il nous reste de beaux jours devant nous, mais cela montre à quel point on est incapable de ne pas reproduire le bug de l'an 2000...

Quand Internet remplace les systèmes experts

Un article paru dans Info-du-net parlant de l'élaboration de diagnostiques pour des maladies montre à quel point la base de données "Internet" peut devenir utile en cas d'utilisation judicieuse :

Un système expert est une base de données de règles et de conditions qui nous amène, en posant des questions sur les symptômes, à un diagnostique précis du problème. C'est donc une base de données contenant tous les symptômes possibles, avec des relations entre eux, que l'on peut questionner. Un système expert n'est utile que si il contient une liste exhaustive des symptômes.

On remarque donc directement une ressemblance frappante avec Internet (ou du moins un moteur de recherche tel que Google) : une base de données que l'on peut questionner.

Internet devient donc un système expert grâce à la contribution des gens dans leurs domaines d'application. Toutefois la différence entre un système expert et Internet, c'est que la base du premier est constituée par des spécialistes et, si elle n'est pas exhaustive, elle est au moins fiable, alors que n'importe bien que la base Internet se met à jour en temps réel, n'importe qui peut y contribuer, même ceux qui n'y connaissent rien au domaine...

Entretien d'embauche avec Google

Les RH de Google m'ont contacté il y a maintenant 3 semaines afin de me faire passer la première étape de leur entretien d'embauche.

L'interview, technique, c'est déroulé en 2 parties de 45 minutes chacune, durant lesquelles un ingénieur Google m'a posé des questions techniques. Apparemment il n'y avait pas un nombre défini de questions, mais tant qu'une réponse jugé satisfaisante était trouvée, on passait à une autre, inventée on the fly mais en relation avec notre CV.

Voici un petit aperçu des 10 questions auxquelles j'ai réussi à répondre. Elles sont traduites en franglais_geek1 pour les besoins du billet, et je n'y fait figurer que celles que j'ai trouvé intéressantes ou qui sont faciles d'exposer sur un blog :

1. Implémentez en C la fonction assert(i > 0) de manière à ce que la condition "i > 0" soit affichée en cas d'erreur
2. Même chose en C++, afin que le code suivant soit bien formé :
   assert(i > 0) << "message" << i ;
3. Triez un tableau d'un million d'entier (int sur 4 bytes) stockée sur un disque dur en ne disposant qu'une mémoire de 2 MB. Comment vous y prenez vous ?
4. Implémentez une classe qui contient 3 méthodes :
   - void push(int)
   - int pop()
   - int minimum()
   dont les 3 méthodes s'exécute avec une complexité en O(1)
5. Trouvez une méthode efficace qui permet de détecter une boucle dans une liste chainée, sans pouvoir modifier les éléments de la liste ni recopier en entier la liste.

Les questions sont posées sans temps de préparation, ni ordinateur ou autres documents d'aide. On remarquera que les réponses, une fois connue, ne sont pas si compliquées qu'elles en auraient l'air.

1. Première hypothèse, avant que l'expert ne précise que la condition "i > 0" doit être affichée :

void assert (int cond) {
  if (cond == 0) {
    printf("Erreur");
    exit(1);
  }
}

Le problème se corse quand il s'agit d'afficher textuellement "i > 0", car en passant par un argument, il sera évalué avant d'être passer par valeur, donc on perd toute chance de pouvoir l'afficher. Ma deuxième version en passant un pointeur de fonction en paramètre s'est vite avérée fastidieuse, et l'idée d'utiliser par une marco et ses possibilités de manipulation de strings m'a soudain frappée, pour finalement donner quelque chose :

#define assert(cond) if ((cond) == 0) { \
  printf("Erreur "); \
  printf(#(cond)); \
  exit(1); \
}

2. Une fois la première question complétée, la deuxième est devenue triviale : il suffit d'ajouter cout à la fin de la macro pour que si la condition était différente de 0, on continue avec cout.

#define assert(cond) if ((cond) == 0) { \
  printf("Erreur "); \
  printf(#(cond)); \
  exit(1); \
} \
cout

3. 1 million d'entiers sur 4 bytes nous fait 4MB, donc trop pour tenir en entier dans la mémoire. Il faut donc partager le tableau en 2, trier chaque partie en utilisant n'importe quel algorithme de tri, puis fusionner les 2 tableaux à l'aide d'un tri par fusion.

4. La complexité en O(1) nous suggère directement l'utilisation d'une liste chainée. Push et pop deviennent donc trivial, push ajoute l'élément à en tête de liste, pop retourne en enlève le premier élément de la liste.
Le problème se pose maintenant pour la méthode qui retourne le minimum, qui est doit aussi se faire en O(1). Il est donc impossible de faire une recherche, car aucune méthode de recherche n'est en O(1). L'idée est donc de maintenir une deuxième liste chainée qui contiendra ces minimums. Donc on modifie push pour tester si la valeur à ajouter est plus petite OU EGALE au minimum, et si c'est le cas on ajoute aussi l'élément dans la liste des minimums, et pop pour enlever l'élément de la liste des minimums si cet élément est le minimum.

En pseudo Java ça nous donne quelque chose du style :

LinkedList l;
LinkedList m;
void push (int e) {
  if (e <= m.top()) {
    m.push(e);
  }
  l.push(e);
}
int pop() {
  int e = l.pop();
  if (e == l.top()) {
    l.pop();
  }
  return e;
}
int minimum() {
  return m.top();
}

5. La solution trivial qui est de marquer les noeuds parcourus n'est pas envisageable, car elle sous-entendrait de modifier le contenu des noeuds, ce qui n'est justement pas possible.
Une bonne solution est donc d'inverser les liens en parcourant la liste, et si on revient au noeud initial on sera sûr d'avoir une boucle. En parcourant la liste dans l'ordre inverse et en réinversant les liens, il est possible de remettre la liste dans l'état qu'on avait avant de débuter la recherche. A noter qu'il est impératif de s'assurer qu'un seul processus n'accède à la liste en simultané, car durant la recherche la liste est modifiée.

2 entretiens sur 6, prochain épisode pour bientôt j'espère...

PHP Multithread

Non, faire tourner PHP en multithread n'est pas un mythe !
C'est possible de lancer des processus fils grâce au module pcntl, et à les synchroniser avec le module sémaphore, de préférence en ligne de commande (la doc précise que leur utilisation en module apache peut amener à des résultats erronés).

Voici donc un petit article qui démontre par un exemple comment implémenter un démon multithread en PHP.